اقرأ المقال الأصلي Modeling Bitcoin’s Value with Scarcity – اقرأ عن نموذج S2FX – تابع الكاتب على تويتر: PlanB
مقدمة
نشر ساتوشي ناكاموتو مستند البيتكوين في 31 أكتوبر 2008[1]، وأطلق الكتلة الأولى في الشبكة بتاريخ 3 يناير 2009، ثم نشر الشيفرة البرمجية في 8 يناير 2009. وبذلك، بدأت رحلة أوصلتنا إلى 70 مليار دولار قيمة سوقية للبيتكوين.
البيتكوين هو أول ابتكار في التاريخ لسلعة رقمية محدودة الكمية. فالبيتكوين محدود الكمية مثل الذهب أو الفضة، ويمكن إرساله عبر الانترنت أو موجات الراديو والأقمار الصناعية وغيرها.
كتجربة ذهنية، تخيل وجود معدن نادر كالذهب ولكن له هذه الخصائص: لونه رمادي باهت، لا يوصل الكهرباء، ليس صلباً، ولا يُستخدم في أغراض صناعية ولا تجميلية.. ولكن تميزه خاصية واحدة سحرية: يمكن إرساله عبر قنوات الاتصالات
ساتوشي ناكاموتو [2]
من المؤكد أن للندرة الرقمية قيمة، ولكن ما مقدار هذه القيمة؟ في هذه المقالة، أستخدم النسبة بين المخزون و التدفق لقياس مقدار الندرة ثم أضع نموذج إحصائي لتقدير قيمة البيتكوين مستنداً إلى نسبة تدفقه إلى مخزونه.
الندرة ونسبة التدفق إلى المخزون
عادة ما تعرّف القواميس الندرة بكونها “شيء يصعبُ الحصول عليه” أو “شيء قليل الوجود”. يُعرّف “نيك سذابو” الندرة في إطار أكثر نفعاً: “تكلفة غير قابلة للتزييف”
ما هي الصفة المشتركة بين الذهب والوقت والأعمال الفنية النادرة؟ ثلاثتهم باهظ التكلفة، ويرجع هذا إما لكلفتهم الأصلية أو لقلة إحتمالية تكرارهم في المستقبل. يصعب التحايل على هذه التكلفة. […] تطبيق مفهوم التكلفة الغير قابلة للتزييف بشكل رقمي ليس بالأمر السهل، ولكنه يحمل في طياته إمكانية التوصل لإختراع الذهب الرقمي [3]
لا يمكن التحايل على ندرة المعادن الثمينة والمقتنيات النادرة، وهذا يرجع لتكلفة انتاجهم. فيما مضى، عندما لعبت المعادن والمقتنيات النادرة دور المال، كان للمال قيمة مستقلة لا يتولى طرف ثالث مسئولية تحديدها. ولكن لا يمكنك استخدام المعادن للسداد عبر الانترنت. ولهذا، فسيكون من الرائع وجود بروتوكول مستقل يجعل من المكلف صنع “بايت” رقمي، ثم يتيح تخزين ونقل والتحقق من صحة هذا البايت الرقمي بطريقة مستقلة ودون الحاجة للثقة بأي طرف: بايت من ذهب [4]
نيك سذابو
يتطلب صك عملات البيتكوين الجديدة إستهلاك كمية كبيرة من الطاقة الكهربائية. ولهذا، فإصدار عملات البيتكوين يتطلب تكلفة غير قابلة للتزييف، والتحايل على عملية إنتاج البيتكوين هو ليس بالأمر السهل. يجدر الإشارة إلى أن هذه الخاصية لا تنطبق على العملات الوطنية كما لا تنطبق على العملات الالكترونية الاخرى التي تفتقر لسقف إمداد أو لنظام لإثبات العمل أو لديها قوة معالجة ضعيفة، أو تخضع لإدارة مجموعة من الناس أو الشركات يمكنهم تعديل قوانينها بسهولة.
يتحدث “سيف الدين عموص” عن الندرة من منظور النسبة بين المخزون و التدفق. فيشرح أن ما يميز الذهب والبيتكوين عن السلع الاخرى كالنحاس والرصاص هو إرتفاع نسبة المخزون مقارنة بالتدفق للذهب والبيتكوين
مضاعفة معدل إنتاج أي سلعة إستهلاكية سيُحجِّم أي مخزون حالي، وسَيتسبَّب بحدوث تحطُّمٍ في الأسعار وسيُلحق الضرر بالمالكين. أما فيما يخص الذهب، فلن يكون ارتفاع الأسعار الذي يؤدي إلى مضاعفة الإنتاج السنوي ذا أهمية، حيث أنه يزيد المخزون بنسبة 3% بدلاً من 1.5%
فمعدل عرض الذهب المنخفض على الدوام هو السبب الجوهري لحفاظه على دوره النقدي على مرّ تاريخ البشرية
فنسبة المخزون إلى التدفق المرتفعة للذهب تجعله السلعة ذات السعر الأقل مرونة بالنسبة للعرض
كانت مخزون عملات البيتكوين المتوفرة عام 2017 أكبر بنحو 25 مرة من العملات الجديدة المُنتجة في نفس العام، ولا يزال هذا أقل من نصف نسبة الذهب، ولكن بحدود عام 2022 ، ستتفوق نسبة المخزون إلى التدفق للبيتكوين على الذهب[5]
سيف الدين عموص
إذاً، فمن الممكن قياس مقدار الندرة بإستخدام النسبة بين المخزون و التدفق (م:ت)
نسبة م:ت = المخزون\التدفق
يشير المخزون إلى حجم الاحتياطي الحالي لأي سلعة بينما يشير التدفق إلى كمية الإنتاج السنوي. قد يستخدم بعض الناس معدل زيادة الإنتاج بدلاً من إستخدام نسبة م:ت. يشير معدل زيادة الإنتاج إلى نسبة التدفق للمخزون: المخزون\التدفق. – لاحظ هنا أن م:ت = 1\معدل زيادة الإنتاج
لنلق نظرة على بعض نسب م:ت
يتمتع الذهب نسبة م:ت=62، وهي الأعلى من بين المعادن؛ يعني هذا أننا سنحتاج إلى 62 سنة من الإنتاج للوصول لحجم المخزون الحالي. يليه الفضة بنسبة م:ت=22. هذه النسبة المرتفعة للمخزون مقارنة بالتدفق هي ما تعطي الذهب والفضة صفة نقدية.

نسبة م:ت لمعادن مثل الباليديوم والبلاتينيوم بالكاد تعلو عن 1؛ فيمكن لحجم إنتاج سنة واحدة أن يضاعف حجم المخزون الحالي. تلعب عملية الإنتاج دوراً هاماً في نسبة م:ت لهذه المعادن. زيادة نسبة م:ت للسلع هو أمر شبه مستحيل نظراً لإرتفاع سعرها بمجرد كنز كميات كبيرة منها، مما يؤدي لزيادة معدل إنتاجها وبالنتيجة عودة سعرها للمعدلات الطبيعية. الإفلات من هذا الفخ هو أمر صعب للغاية.
مخزون البيتكوين الحالي هو 17.5 مليون عملة، وتُصَّك العملات الجديدة بمعدل 0.7 مليون عملة في السنة – مما يعطينا نسبة م:ت = 25. تضع هذه النسبة البيتكوين في فئة السلع النقدية مثل الذهب والفضة. تقدر القيمة السوقية لعملات البيتكوين ب$70 مليار دولار
تُصدر عملات البيتكوين وفق جدول زمني ثابت. تعالج الشبكة كتلة جديدة من التحويلات كل 10 دقائق في المتوسط وتتضمن هذه الكتل العملات الجديدة. فعندما يحل أحد المعدنين المسألة الرياضية لنظام إثبات العمل للكتلة، يحصل على تلك العملات الجديدة والمسماة ـ”دعم الكتلة”. تشتمل مكافئة الكتلة على دعم الكتلة إضافة على كل رسوم التحويل المتضمنة من قبل المرسلين.
بدأ دعم الكتلة ب 50 بيتكوين لكل كتلة، وتقل للنصف كل 210,000 كتلة (حوالي 4 أعوام). يطلق على هذه العملية أسم “التنصيف”، وهي أمر هام للغاية بالنسبة للعرض النقدي للبيتكوين ونسبة م:ت. عملية التنصيف هي ما يجعل التغيير بمعدل زيادة العرض يحدث في خطوات حادة، بدلاً من تغير ناعم. (في عالم البيتكوين، يُطلق على معدل زيادة العرض مصطلح “التضخم النقدي”)
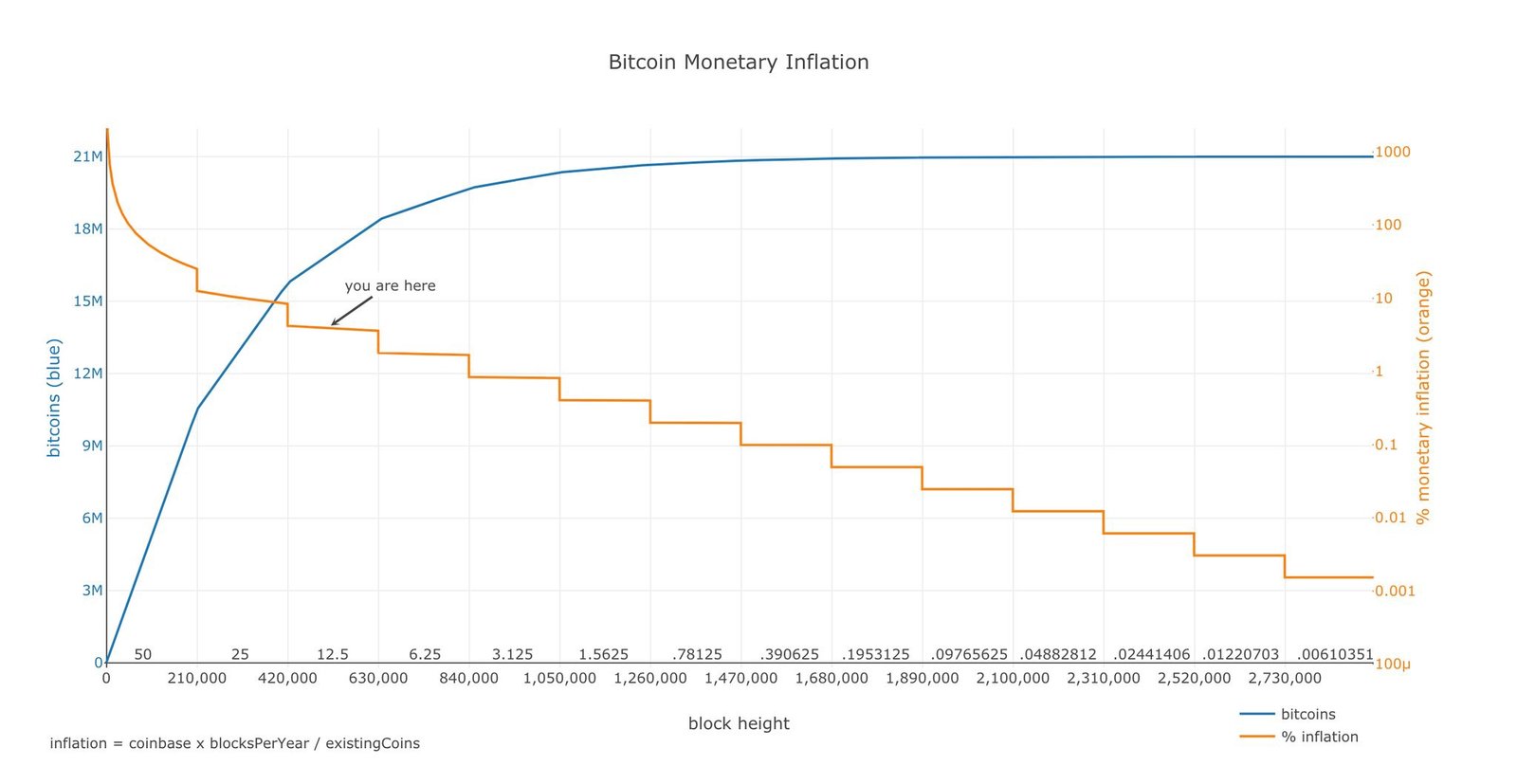
نسبة المخزون إلى التدفق والقيمة
الفرضية في هذا البحث هي أن الندرة، مُعرفة في إطار نسبة المخزون إلى التدفق، تؤثر بشكل مباشر في القيمة. إلقاء نظرة على الجدول أعلاه يؤكد أن القيمة السوقية تميل للزيادة مع زيادة نسبة المخزون إلى التدفق. الخطوة التالية هي جمع البيانات ووضع نموذجاً إحصائياً.
البيانات
قمت بحساب نسبة م:ت والقيمة السوقية للبيتكوين لكل الشهور من ديسيمبر 2009 حتى فبراير 2019 ( بمجموع 111 نقطة قياس). يمكن استخراج عدد الكتل لكل شهر من سلسلة كتل البيتكوين بإستخدام أمر Python/RPC/bitcoind. يختلف عدد الكتل الفعلي عن المعدل النظري، ويرجع هذا لأن الكتل لا تُصدر كل 10 دقائق بدقة. (مثلاً، كان عدد الكتل في عام 2009 أقل بكثير من المعدل النظري)
وبإستخدام عدد الكتل المُصدرة كل شهر والمعدل المعروف لدعم الكتلة، يمكننا حساب التدفق والمخزون. أخرجت أول مليون عملة من الحسابات (7 شهور) وذلك بغرض التصحيح لمراعاة العملات المفقودة. ستكون مسألة التعديل لمراعاة العملات المفقودة موضوعاً للبحث المستقبلي.
تتوفر البيانات عن سعر البيتكوين من عدة مصادر ولكنها تبدأ في شهر يوليو 2010. استخدمت أول عمليات تسعير للبيتكوين قبل هذا التاريخ من أجل إكمال الحسابات (دولار واحد لقاء 1309 عملة في اكتوبر 2009 – 0.003 دولار للعملة في مارس 2010، وعملية بيع شطيرتي بيتزا بقيمة 41 دولار لقاء 10,000 عملة بيتكوين في مايو 2010). سيكون إستكشاف البيانات القديمة موضوعاً للبحث المستقبلي.
لدينا بالفعل البيانات الخاصة بالذهب (م:ت 62 وقيمة سوقية 8.5 تريليون دولار) وللفضة (م:ت 22 وقيمة سوقية 308 مليار دولار)؛ سأستخدم هذه البيانات كمقياس مرجعي.
النموذج الإحصائي
بوضع رسم إحصائي بالنقاط المبعثرة، يتبين لنا وجوب إستخدام المقياس اللوغاريتمي لعرض القيمة السوقية، وذلك لتضاعفها 8 مرات (من $10 آلالف إلى $100 مليار). وبإستخدام المقياس اللوغاريتمي أيضاً لنسبة م:ت، يتبين لنا وجود علاقة خطية جيدة بين اللوغاريتم الطبيعي لكل من م:ت و القيمة السوقية. (لاحظ أن إستخدام لوغاريتم عشري سيحقق نتائج مماثلة)
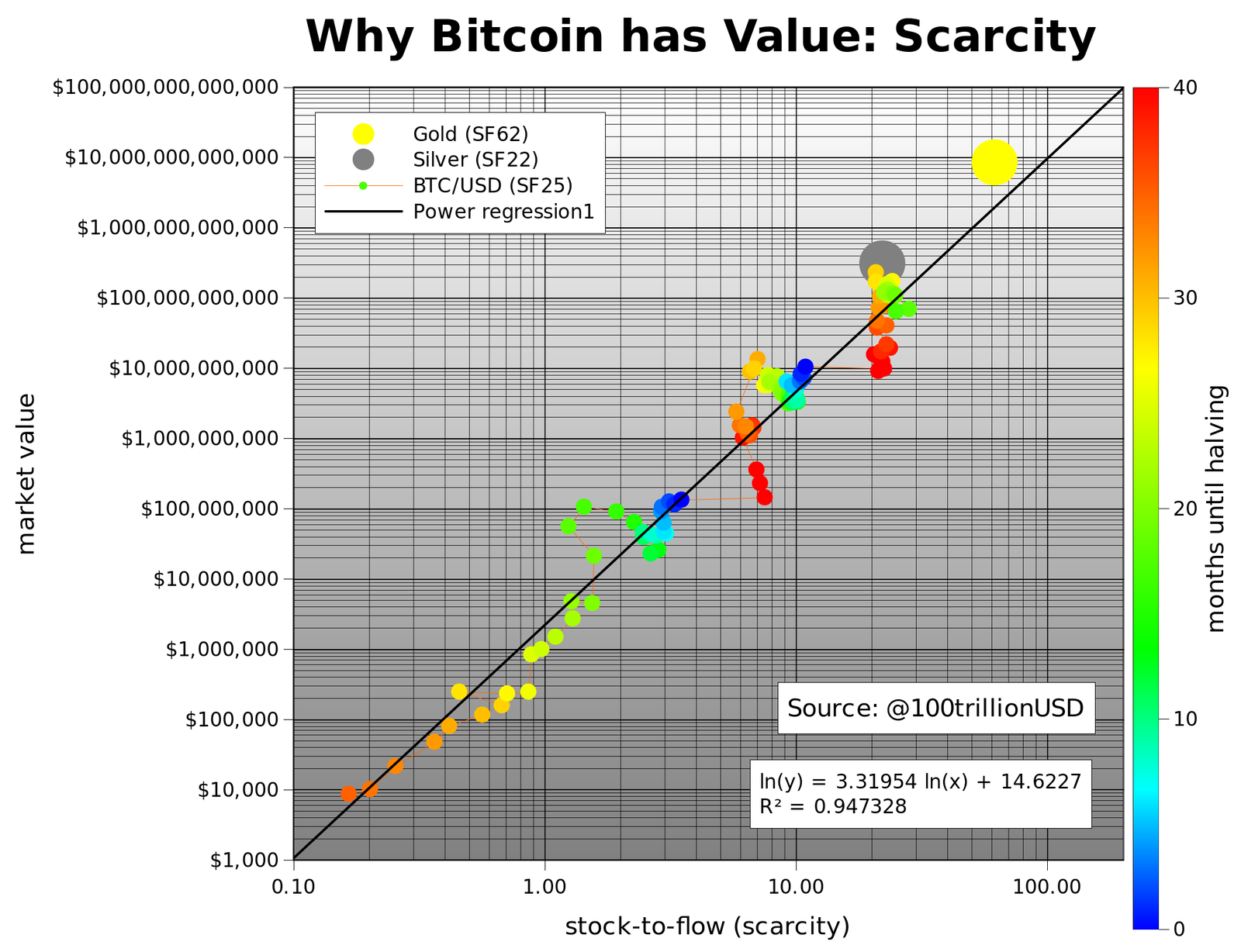
يؤكد الإنحدار الخطي ما يمكن رؤيته بالعين المجردة: علاقة ذات دلالة إحصائية بين نسبة م:ت والقيمة السوقية للبيتكوين (معامل التحديد 95% – القيمة الاحتمالية 2.3E-17 – القيمة الاحتمالية للانحدار 2.3E-17). فإحتمال كون العلاقة بينهما محض صُدفةً أو عَرَضًا هو أقرب إلى الصفر. تؤثر عوامل أخرى على السعر مثل القوانين الحكومية وعمليات القرصنة والاخبار المختلفة، ولهذا لا تصل قيمة معامل التحديد إلى 100% (أي أنه لا تقع كل النقاط على خط مستقيم بدقة تامة). ولكن يبدو أن الندرة (نسبة م:ت) هي العامل المهيمن.[i]
ومن المثير للدهشة هو أنه وبالرغم من كونهما أسواق مختلفة تماماً، تتماشى القيمة السوقية للذهب والفضة مع قيمة البيتكوين التي يقدمها النموذج. يعزز هذا الأمر الثقة بالنموذج الإحصائي. لاحظ أنه في أوج السوق الصاعدة للبيتكوين في ديسيمبر 2017، كانت نسبة م:ت 22 وكانت القيمة السوقية $230 مليار وهي أرقام مقاربة جداً للفضة.
ولأن للتنصيف أثر كبير على نسبة م:ت، قمت بتلوين الشهور بحسب قربها من موعد التنصيف على النحو التالي: شهور التنصيف بالون الأزرق الغامق، والأحمر للشهور بُعَيدَ التنصيف. موعد التنصيف القادم في شهر مايو 2020. ونسبة م:ت الحالية ستضاعف من 25 لتصبح 50، وهذه النسبة قريبة جداً من النسبة الخاصة بالذهب وهي 62
تبلغ القيمة السوقية المُقدرة للبيتكوين بعد تنصيف مايو 2020 تريليون دولار، وهو ما يمثل سعر 55 ألف دولار لعملة البيتكوين الواحدة، سيكون هذا أمراً رائعاً. سيخبرنا الزمن بعد مرور سنة أو أثنين على التنصيف، بحلول عام 2020 أو 2021، ما إذا كان هذا التقدير صحيحاً، فالأمر بمثابة أول إختبار للفرضية والنموذج من خارج العينة المعروفة.
يسألني الناس من أين سيأتي المال المطلوب للوصول إلى قيمة سوقية بحجم تريليون دولار؟ ستأتي الأموال من مصادر عدة: من الذهب والفضة، ومن البلدان ذات معدلات الفائدة السالبة (كأوروبا واليابان وقريباً الولايات المتحدة)، ومن البلاد ذات الحكومات الإستغلالية (كالصين وفينيزويلا وإيران وتركيا وغيرهم)، ومن أصحاب الثروات الكبيرة للتحوط ضد التيسير الكمي (أي ضخ البنوك المركزية للسيولة المالية وطباعة نقد جديد)، وأخيراً من المؤسسات الإستثمارية عندما تكتشف أفضل الأصول أداءً في العشر سنين الأخيرة.
بوسعنا أيضاً التنبؤ بسعر عملة البيتكوين مباشرة من نسبة م:ت. ستختلف معايير المعادلة الرياضية ولكن تبقى النتيجة ذاتها: معامل التحديد 95% وسعر عملة بيتكوين متوقع يبلغ $55000 مع وصول نسبة م:ت إلى 50، وذلك بعد تنصيف مايو 2020
وضعت رسم بياني للسعر المتوقع بناء على نسبة م:ت (باللون الأسود) و سعر البيتكوين الحقيقي ملوناً بحسب عدد الكتل المُنتجة في الشهر.
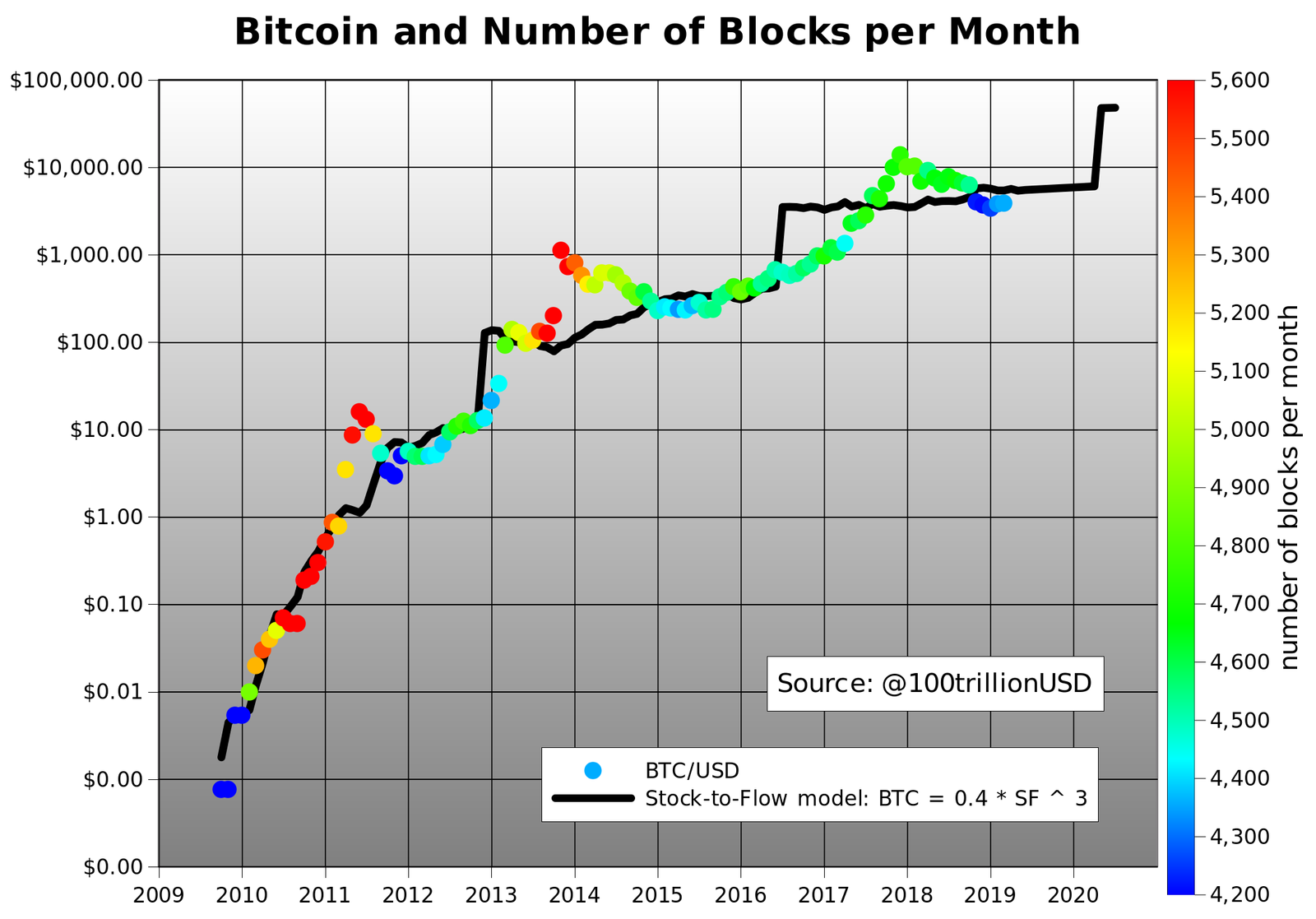
لاحظ مدى مطابقة السعر الحقيقي للمتوقع. يتضح التوافق جلياً في سرعة تكيف الأسعار بعد تنصيف نوفمبر 2012. كانت عملية تكيف الأسعار مع تنصيف يونيو 2016 أبطأ بكثير، وهذا على الأرجح بسبب المنافسة من العملات الأخرى كالإيثيريوم وإختراق DAO الأمني. يمكنك أيضاً رؤية إنخفاض عدد الكتل المُنتجة في الشهر (باللون الأزرق) في أول عمل الشبكة في 2009 و مع تدني صعوبة التعدين في نهاية 2011، منتصف 2015 ونهاية 2018. أدى إستخدام كروت الجرافيك في 2010-2011 والمعالجات المحددة برمجياً (AISCs) في 2013 إلى تزايد عدد الكتل المُنتجة في الشهر (باللون الأحمر)
قوانين القوة والأنماط الهندسية المتكررة (Fractals)
وجود دلالة على علاقة قوة هو أمر مثير للإهتمام جداً
دالة الإنحدار الخطي[ii] هي: ln(market value) = 3.3 * ln(SF)+14.6
يمكن كتابتها كدالة قانون قوة[iii]: القيمة السوقية = exp(14.6) * SF ^ 3.3
إمكانية إيجاد علاقة قوة ممتدة عبر 8 مضاعفات للسعر وبمعامل تحديد 95% هو أمر يعزز الثقة بالنموذج الإحصائي ويدعم فرضية أن نسبة م:ت هي المحرك الرئيسي لقيمة البيتكوين.
يشير قانون القوة إلى علاقة بين متغيرين بحيث يؤدي تغيير قيمة المتغير الأول إلى تغيير متناسب له في الثاني، بغض النظر عن القيمة الأولية لهذه المتغيرات. بعبارة أخرى، مع كل عملية تنصيف تتضاعف نسبة م:ت للبيتكوين وتزداد قيمته السوقية بعشرة أضعاف، هذه العلاقة ثابتة.
علاقات القوة مثيرة للإهتمام لأنها تكشف عن آلية نظامية لخواص نظام يبدو في ظاهره معقد وعشوائي. أنظر التذييل للاطلاع على بعض أشهر الأمثلة على قانون القوة. عادة ما تكون للأنظمة المعقدة خواص تجعل نسب التغيرات بين الظواهر ثابتة بغض النظر عن حجم تلك الظواهر.
هذا النمط المتكرر يكمن وراء علاقات قانون القوة. نرى هذا الأمر في البيتكوين: فإنهيار الأسعار في أعوام 2011، 2014 و 2018 تبدو كلها متشابهة (-80% في كل مرة) ولكن على مقاييس مختلفة تماماً ($10 و$1000 و $10000)؛ لا يمكنك رؤية هذا الأمر إن لم تستخدم مقياس لوغاريتمي. هذا التشابه الذاتي وثبات نسب التغيير له علاقة بالأنماط الهندسية المتكررة. في الواقع فإن قيمة 3.3 في دالة الإنحدار الخطي أعلاه هي “البعد الكسوري”. للمزيد من المعلومات عن الأنماط الهندسية المتكررة أنظر الدراسة الشهيرة لطول الخطوط الساحلية.[7]
الخلاصة
البيتكوين هو أول ابتكار في التاريخ لسلعة رقمية محدودة الكمية. فالبيتكوين محدود الكمية مثل الذهب أو الفضة، ويمكن إرساله عبر الانترنت أو موجات الراديو والأقمار الصناعية وغيرها.
من المؤكد أن للندرة الرقمية قيمة، ولكن ما مقدار هذه القيمة؟ في هذه المقالة، أستخدم نسبة المخزون إلى التدفق لقياس مقدار الندرة ثم أضع نموذج إحصائي لتقدير قيمة البيتكوين مستنداً لنسبة تدفقه إلى مخزونه.
هناك علاقة ذات دلالة إحصائية بين نسبة م:ت والقيمة السوقية للبيتكوين، فإحتمال كون العلاقة بينهما محض صُدفةً أو عَرَضًا هو أقرب إلى الصفر.
ومما يزيد الثقة في النموذج:
بالرغم من كونهما أسواق مختلفة تماماً، تتماشى القيمة السوقية للذهب والفضة مع قيمة البيتكوين التي يقدمها النموذج
وهناك مؤشرات على كون العلاقة علاقة قوة (بمعنى أن معامل التغيير ثابت بين نسبة م:ت و بين القيمة، بغض النظر عن حجمهما)
يتنبأ النموذج أن تصل القيمة السوقية للبيتكوين إلى ترليون دولار أمريكي بعد التنصيف المقبل في عام 2020، وهو ما يمثل سعر 55 ألف دولار لعملة البيتكوين الواحدة.
مراجع
[1] https://bitcoin.org/bitcoin.pdf — Satoshi Nakamoto, 2008
[2] https://bitcointalk.org/index.php?topic=583.msg11405#msg11405 — Satoshi Nakamoto, 2010
[3] https://unenumerated.blogspot.com/2005/10/antiques-time-gold-and-bit-gold.html — Nick Szabo, 2008
[4] https://unenumerated.blogspot.com/2005/12/bit-gold.html — Nick Szabo, 2008
[5] The Bitcoin Standard: The Decentralized Alternative to Central Banking — Saifedean Ammous, 2018 – كتاب معيار البيتكوين – د. سيف الدين عموص
[6] https://necsi.edu/power-law
[7] http://fractalfoundation.org/OFC/OFC-10-4.html
[i] (95% R2, significance of F 2.3E-17, p-Value of slope 2.3E-17)
[ii] The linear regression function: ln(market value) = 3.3 * ln(SF)+14.6
[iii] Power law function: market value = exp(14.6) * SF ^ 3.3





2 تعليقات